Since the advent of multicore CPUs in the mid-2000s, the ability of computers to perform calculations has improved much faster than their ability to move data. The latter often becomes a bottleneck when the product of a large, sparse matrix and a vector is computed, which is a common operation in scientific codes. In many algorithms, these products are repeated multiple times with the same matrix. This so-called matrix-power kernel (MPK) offers an opportunity to cut down on unnecessary data movement, since the same data is used over and over again. Only recently has this potential been tapped successfully with the Recursive Algebraic Coloring Engine (RACE), which analyzes the underlying graph of the matrix to determine an efficient order for calculating the elements of the result vectors. Until now, however, the data dependencies have limited this approach to a single computing node. Extending the MPK to work efficiently across multiple nodes for large-scale simulations is challenging because it requires careful coordination and communication of data.
Recently, an NHR@FAU team has developed a flexible method that combines the data-reuse advantages of RACE with a new multi-node communication scheme to meet these demands. The improved MPK algorithm delivers significant speed-ups on modern CPU architectures across a wide range of sparse matrices. An application from physics that was shown to benefit from this is the Chebyshev method for the time-evolution of quantum systems.
For more information, see the publication in The International Journal of High Performance Computing Applications:
Cache blocking of distributed-memory parallel matrix power kernels
Dane Lacey, Christie Alappat, Florian Lange, Georg Hager, Holger Fehske, and Gerhard Wellein
The International Journal of High Performance Computing Applications. 2025; 39 (3): 385 – 404
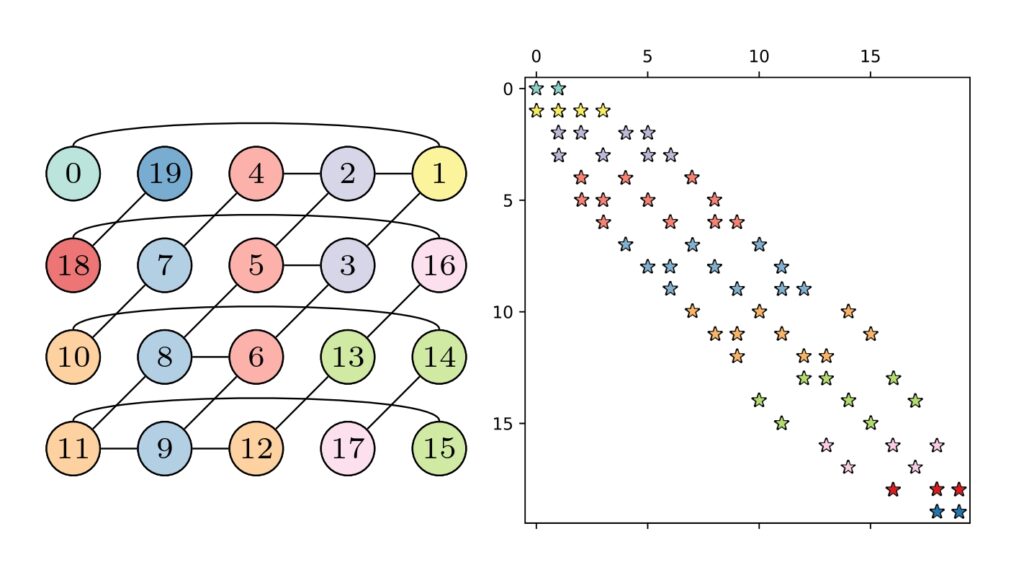
Since the advent of multicore CPUs in the mid-2000s, the ability of computers to perform calculations has improved much faster than their ability to move data. The latter often becomes a bottleneck when the product of a large, sparse matrix and a vector is computed, which is a common operation in scientific codes. In many algorithms, these products are repeated multiple times with the same matrix. This so-called matrix-power kernel (MPK) offers an opportunity to cut down on unnecessary data movement, since the same data is used over and over again. Only recently has this potential been tapped successfully with the Recursive Algebraic Coloring Engine (RACE), which analyzes the underlying graph of the matrix to determine an efficient order for calculating the elements of the result vectors. Until now, however, the data dependencies have limited this approach to a single computing node. Extending the MPK to work efficiently across multiple nodes for large-scale simulations is challenging because it requires careful coordination and communication of data.
Recently, an NHR@FAU team has developed a flexible method that combines the data-reuse advantages of RACE with a new multi-node communication scheme to meet these demands. The improved MPK algorithm delivers significant speed-ups on modern CPU architectures across a wide range of sparse matrices. An application from physics that was shown to benefit from this is the Chebyshev method for the time-evolution of quantum systems.
For more information, see the publication in The International Journal of High Performance Computing Applications:
Cache blocking of distributed-memory parallel matrix power kernels
Dane Lacey, Christie Alappat, Florian Lange, Georg Hager, Holger Fehske, and Gerhard Wellein
The International Journal of High Performance Computing Applications. 2025; 39 (3): 385 – 404