From gravity to electromagnetism, algebraically decaying long-range interactions are ubiquitous in nature. In the context of quantum many-body systems, repulsive algebraically decaying long-range interactions are relevant in a variety of analogue quantum simulation platforms based on atomic or molecular quantum optics systems such as trapped ions, ultracold trapped dipolar gases, or Rydberg-atom quantum simulators. In lattice models repulsive long-range interactions give rise to an infinite staircase (devil’s staircase) of crystalline phases.
In their recent publication Jan Alexander Koziol, Anja Langheld, and FAU LMQ member Kai Pillip Schmidt studied the fundamental question of how such devil’s staircases melt when the matter degrees of freedom are linearly coupled to a single bosonic mode. In the context of light-matter quantum systems, this setup can serve as a toy model for the coupling of long-range interacting matter degrees of freedom to a single photonic (cavity) mode. With their quantitative analysis the authors revealed combined light-matter phases at intermediate light-matter coupling in the melting process that arise from the interplay between matter-matter and light-matter interactions. Further, the authors calculated quantitative quantum phase diagrams and characterized the occurring quantum phase transitions. This research effort provides insight into the engineering of complex quantum states with an interplay between long-range matter-matter and light-matter interactions.
For more information, see their publication in Physical Review B:
Melting of devil’s staircases in the long-range Dicke-Ising model
Jan Alexander Koziol, Anja Langheld, Kai Phillip Schmidt
Physical Review B 111, 224427 (2025)
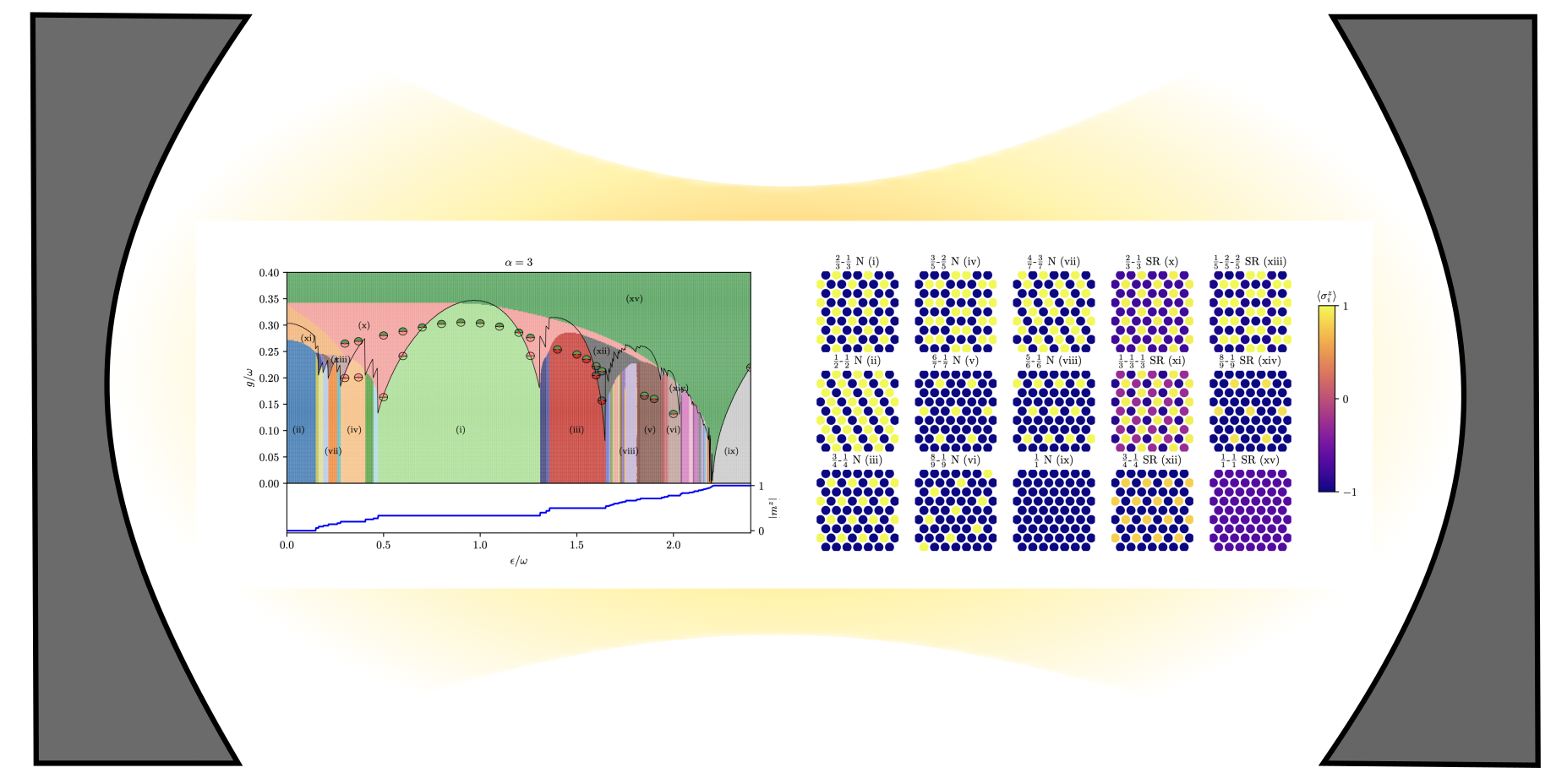
From gravity to electromagnetism, algebraically decaying long-range interactions are ubiquitous in nature. In the context of quantum many-body systems, repulsive algebraically decaying long-range interactions are relevant in a variety of analogue quantum simulation platforms based on atomic or molecular quantum optics systems such as trapped ions, ultracold trapped dipolar gases, or Rydberg-atom quantum simulators. In lattice models repulsive long-range interactions give rise to an infinite staircase (devil’s staircase) of crystalline phases.
In their recent publication Jan Alexander Koziol, Anja Langheld, and FAU LMQ member Kai Pillip Schmidt studied the fundamental question of how such devil’s staircases melt when the matter degrees of freedom are linearly coupled to a single bosonic mode. In the context of light-matter quantum systems, this setup can serve as a toy model for the coupling of long-range interacting matter degrees of freedom to a single photonic (cavity) mode. With their quantitative analysis the authors revealed combined light-matter phases at intermediate light-matter coupling in the melting process that arise from the interplay between matter-matter and light-matter interactions. Further, the authors calculated quantitative quantum phase diagrams and characterized the occurring quantum phase transitions. This research effort provides insight into the engineering of complex quantum states with an interplay between long-range matter-matter and light-matter interactions.
For more information, see their publication in Physical Review B:
Melting of devil’s staircases in the long-range Dicke-Ising model
Jan Alexander Koziol, Anja Langheld, Kai Phillip Schmidt
Physical Review B 111, 224427 (2025)