Strongly correlated electron materials are notoriously difficult to treat as, by definition, most of their properties cannot be predicted by mapping the quantum many-body problem to auxiliary single particle models (as done, e.g. in density functional theory) or perturbation theory. However, the plethora of exciting emergent phenomena seen in such materials – such as high-temperature superconductivity in cuprates – is a great motivation to take on this challenge anyway.
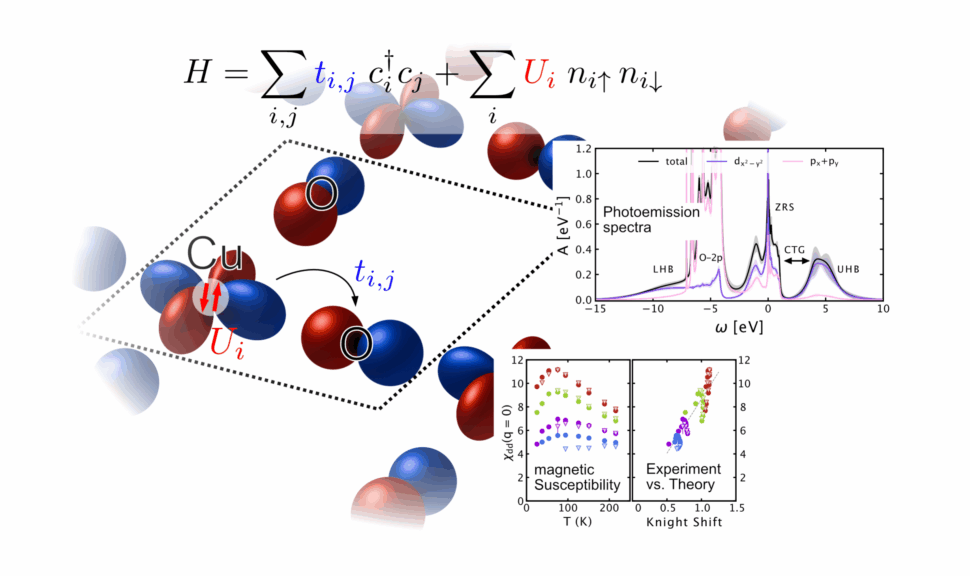
Specifically, one wants to explain and/or predict observables that can be directly measured experimentally. In their recent work, Yi-Ting Tseng, Mário O. Malcoms, Henri Menke, Marcel Klett, Thomas Schäfer, and Philipp Hansmann investigate the so-called Emery model which has been suggested to capturing correctly the ground state of high Tc cuprates as well as excitations on the eV scale. Different from the single band Hubbard model which is also frequently used to explain cuprate physics, the Emery model includes oxygen degrees of freedom explicitly. Exact solution is impossible and perturbative- or static mean-field methods are known to perform poorly. In the present paper they use dynamical mean-field theory (DMFT) and focus on the magnetic susceptibility which can be measured in nuclear magnetic resonance (NMR) experiments (via the so-called Knight shift). They find that DMFT not only reproduces the downturn of the uniform spin susceptibility in the pseudogap regime, but also captures its doping and temperature trends in very good agreement with experiment. This implies that at least part of the observed non-Curie-like behavior originates from local correlations, since single-site DMFT neglects non-local ones. The latter are, however, essential to account for the momentum-dependent gapping of the Fermi surface—the emergence of “Fermi arcs”—that defines the pseudogap phase. Their results therefore suggest that while the susceptibility downturn and Fermi arcs may be related phenomena, a substantial part of the susceptibility behavior can already be explained by very short-range correlations. Importantly, DMFT applied to the simpler single-band Hubbard model captures neither the non-Curie susceptibility nor the Fermi arcs, underscoring the crucial role of explicitly including oxygen degrees of freedom.
In a broader context, the study illustrates the general difficulty of connecting theory with experiment in the presence of strong electronic correlations: when discrepancies arise, it is often unclear whether they point to shortcomings of the model itself, or to the limitations of the approximation used to solve it.
For more information, see their publication in SciPost Physics:
Single-particle spectra and magnetic susceptibility in the Emery model: A dynamical mean-field perspective
Yi-Ting Tseng, Mário O. Malcolms, Henri Menke, Marcel Klett, Thomas Schäfer, Philipp Hansmann
SciPost Phys. 18, 145 (2025)
Strongly correlated electron materials are notoriously difficult to treat as, by definition, most of their properties cannot be predicted by mapping the quantum many-body problem to auxiliary single particle models (as done, e.g. in density functional theory) or perturbation theory. However, the plethora of exciting emergent phenomena seen in such materials – such as high-temperature superconductivity in cuprates – is a great motivation to take on this challenge anyway.
Specifically, one wants to explain and/or predict observables that can be directly measured experimentally. In their recent work, Yi-Ting Tseng, Mário O. Malcoms, Henri Menke, Marcel Klett, Thomas Schäfer, and Philipp Hansmann investigate the so-called Emery model which has been suggested to capturing correctly the ground state of high Tc cuprates as well as excitations on the eV scale. Different from the single band Hubbard model which is also frequently used to explain cuprate physics, the Emery model includes oxygen degrees of freedom explicitly. Exact solution is impossible and perturbative- or static mean-field methods are known to perform poorly. In the present paper they use dynamical mean-field theory (DMFT) and focus on the magnetic susceptibility which can be measured in nuclear magnetic resonance (NMR) experiments (via the so-called Knight shift). They find that DMFT not only reproduces the downturn of the uniform spin susceptibility in the pseudogap regime, but also captures its doping and temperature trends in very good agreement with experiment. This implies that at least part of the observed non-Curie-like behavior originates from local correlations, since single-site DMFT neglects non-local ones. The latter are, however, essential to account for the momentum-dependent gapping of the Fermi surface—the emergence of “Fermi arcs”—that defines the pseudogap phase. Their results therefore suggest that while the susceptibility downturn and Fermi arcs may be related phenomena, a substantial part of the susceptibility behavior can already be explained by very short-range correlations. Importantly, DMFT applied to the simpler single-band Hubbard model captures neither the non-Curie susceptibility nor the Fermi arcs, underscoring the crucial role of explicitly including oxygen degrees of freedom.
In a broader context, the study illustrates the general difficulty of connecting theory with experiment in the presence of strong electronic correlations: when discrepancies arise, it is often unclear whether they point to shortcomings of the model itself, or to the limitations of the approximation used to solve it.
For more information, see their publication in SciPost Physics:
Single-particle spectra and magnetic susceptibility in the Emery model: A dynamical mean-field perspective
Yi-Ting Tseng, Mário O. Malcolms, Henri Menke, Marcel Klett, Thomas Schäfer, Philipp Hansmann
SciPost Phys. 18, 145 (2025)